One important application of PCA to the study of interstellar
structure has been given by HB99, who compute a
velocity increment-size relation from the
PCA results for a number of ``pseudo-simulations'', in which random
velocity fields with prescribed energy spectra of index ![]() are
constructed. In this section we
derive an analogous correlation for the simulation data.
The velocity increment-size relation can be extracted from the
PCA results by computing the autocorrelation function of each
eigenvector, and for its corresponding eigenimage. For each of these, a
characteristic (velocity or spatial) scale can be defined as
the lag at which the correlation has decayed to a prescribed value. A
velocity increment-size relation can then be obtained by plotting the pairs
of characteristic velocity and spatial scales for all eigenvectors. In
practice, only the data for the most statistically significant principal
components are retained. The spatial autocorrelation is defined by
are
constructed. In this section we
derive an analogous correlation for the simulation data.
The velocity increment-size relation can be extracted from the
PCA results by computing the autocorrelation function of each
eigenvector, and for its corresponding eigenimage. For each of these, a
characteristic (velocity or spatial) scale can be defined as
the lag at which the correlation has decayed to a prescribed value. A
velocity increment-size relation can then be obtained by plotting the pairs
of characteristic velocity and spatial scales for all eigenvectors. In
practice, only the data for the most statistically significant principal
components are retained. The spatial autocorrelation is defined by
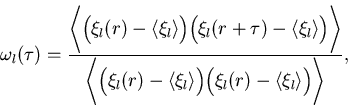 |
(1) |
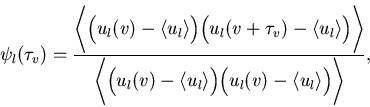 |
(2) |
Figures 6a and 6b show the ![]() -R relation obtained for the
simulation data, for two different values of the fraction
-R relation obtained for the
simulation data, for two different values of the fraction ![]() . HS97
and HB99 use
. HS97
and HB99 use
![]() (fig. 6a), but since our correlations
exhibit stronger fluctuations than theirs, we also use
(fig. 6a), but since our correlations
exhibit stronger fluctuations than theirs, we also use
![]() (fig. 6b). We note that the slope
(fig. 6b). We note that the slope ![]() of the velocity
dispersion-size curve for the simulations depends on
of the velocity
dispersion-size curve for the simulations depends on ![]() .
At
.
At
![]() (fig. 6a), a least-squares fit
gives
(fig. 6a), a least-squares fit
gives
![]() , while at
, while at
![]() (fig. 6b) we find
(fig. 6b) we find
![]() . Interestingly, these values seem to follow the
relation
. Interestingly, these values seem to follow the
relation
![]() , since the energy spectrum of the
simulation, shown in fig. 7, is not a perfect power law (because of
the low resolution). Instead, the slope is shallower (
, since the energy spectrum of the
simulation, shown in fig. 7, is not a perfect power law (because of
the low resolution). Instead, the slope is shallower (![]() ) at
small wave numbers (i.e., larger scales) and steeper (
) at
small wave numbers (i.e., larger scales) and steeper (![]() ) at
larger wavenumbers (smaller scales). On the other hand, usage of a
lower threshold
) at
larger wavenumbers (smaller scales). On the other hand, usage of a
lower threshold ![]() on the correlation function implies including
the contribution from larger scales, so the appropriate spectral slope
should be that for the large scales. Indeed, in this case,
on the correlation function implies including
the contribution from larger scales, so the appropriate spectral slope
should be that for the large scales. Indeed, in this case,
![]() and
and
![]() . Conversely, using the larger threshold
. Conversely, using the larger threshold
![]() takes into account the contribution of the small scales
only, and in this case
takes into account the contribution of the small scales
only, and in this case
![]() and
and
![]() . In both
cases,
. In both
cases,
![]() . Higher spatial and velocity resolutions
are necessary to confirm this result.
. Higher spatial and velocity resolutions
are necessary to confirm this result.