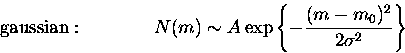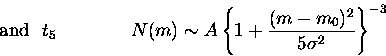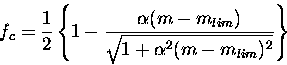Next: About this document ...
Globular Cluster Luminosity Function Analysis
Pablo G. Ostrov
Facultad de Ciencias Astronómicas y Geofísicas, Paseo del Bosque
S/N (1900) La Plata, Argentina
ostrov@fcaglp.fcaglp.unlp.edu.ar
http://www.fcaglp.unlp.edu.ar/~ostrov/
INTRODUCTION.
One of the most common problems of astronomical work is that of
distance determination. Astronomers wish to find
objects bright enough to be useful as standard candles.
Undoubtedly, globular clusters are bright enough to be
considered potentially interesting objects for distance
determination. The obstacle arising from the broad range that they
span in luminosity brightness can be avoided by observing samples
of many of them, and then using the globular cluster luminosity
function (GCLF) as a standard candle.
Harris, Allwright,
Pritchet and van den Bergh (1991) analyzed
observations of three Virgo giant ellipticals, founding no
noticeable differences between their GCLFs.
In virtue of the progressive advance of astronomical
technology, it has been feasible to study globular cluster systems
of an increasing sample of galaxies. It is now possible to begin
to investigate the second order differences between GCLFs, and its
relations with their environments and metallicities.
MOTIVATION
From a practical point of view, the determination of GCLF
parameters presents several problems:
1.- One frequently observes the bright half of the luminosity
distribution, and losses an usually significant fraction of the
faint half.
2.- The sample of globulars is unavoidably contaminated by
interlopers, and this contamination must be removed by means of
some statistical consideration. Only in several nearby galaxies is
feasible, with space telescope observations, to resolve the
globulars and thus to distinguish them from foreground stars and
unresolved background objects.
The aim of this work is to investigate the credibility of GCLF
parameter determinations, and how incompleteness and contamination
affect the results. It is needed to answer some basic questions,
as how many magnitudes deeper than the turn-over it is required
to observe to obtain reliable parameter estimates, and how many
clusters should have a sample to be suitable for GCLF analysis.
NUMERICAL EXPERIMENTS
In order to answer the above formulated questions, series of
observed luminosity distribution models were generated. These
models were analyzed by means of a maximum likelihood method (Secker
& Harris, 1993) that allows to obtain simultaneously the peak of
the luminosity distribution m0 and the dispersion 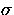 . A previous
work was performed by Hanes & Whittaker (1987),
addressed
specifically to GCSs at distances such as the Virgo Cluster.
. A previous
work was performed by Hanes & Whittaker (1987),
addressed
specifically to GCSs at distances such as the Virgo Cluster.
PARAMETERS OF MODELS
GCLF: Two types of distributions were generated
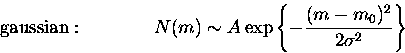
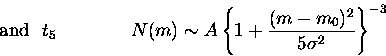
Completeness: It was modeled by means of a Pritchet function
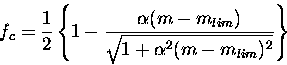
where mlim stands for the 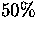 completeness level magnitude and
the shape parameter
completeness level magnitude and
the shape parameter 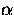 was chosen to be equal to 2.4.
was chosen to be equal to 2.4.
Ngc: Regarding the total number of globular clusters Ngc, three
series of models were generated with 400, 2000 and 10000 globulars
each one.
mcut: It represents the faintest magnitude at which the data are
considered useful. Surpassing this limit, all data are removed and
the completeness factor is set to zero. Series of models with mcut
equivalent to 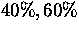 and
and 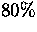 of completeness were generated.
of completeness were generated.
Background: The background population was modeled by means of the
distribution
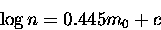
The slope was obtained by least squares fitting to a real
background data sample and the density of background objects was
chosen according to realistic cases. For each model a separate
``background data set'' was generated to simulate the ``background
field'' used for background contamination correction.
m0: Samples with luminosity function peak at 23.25, 23.75, 24.25
and 24.75 were generated. These corresponds to distances ranging
from 16 Mpc to 40 Mpc approximately.
Initial conditions: Being the analysis based on a maximum
likelihood method, the solution converges to a local maximum. For
this reason, the influence of the starting guesses on the results
were also investigated.
A total of 1000 data sets were generated for each model,
therefore the following results comprise the analysis of more
than one million of fittings.
RESULTS
1.- Choice of mcut:
The choice of mcut is not a critical one. In the cases in which
some systematic behavior of
the errors is noticeable, the better results are obtained for the
faintest mcut.
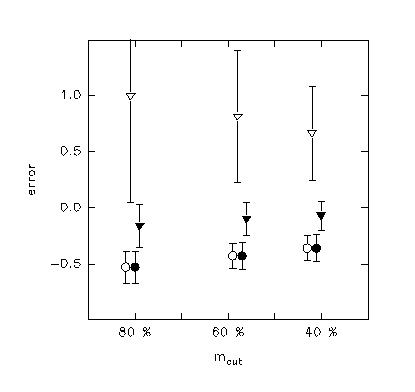
Figure 1 shows an example of the dependence of errors in m0
fittings for different value of mcut. Circles correspond to
gaussian models and triangles to t5 models. Hollow symbols stand
for gaussian fittings and filled symbols stand for t5 fittings.
2.- In which cases the estimates for 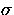 are reliable?
are reliable?
The accurate determination of  is feasible only if the
peak of the luminosity function has been surpassed by, at least,
two magnitudes. Even in such cases, errors of
is feasible only if the
peak of the luminosity function has been surpassed by, at least,
two magnitudes. Even in such cases, errors of  occur if
the contamination of the sample is meaningful.
occur if
the contamination of the sample is meaningful.
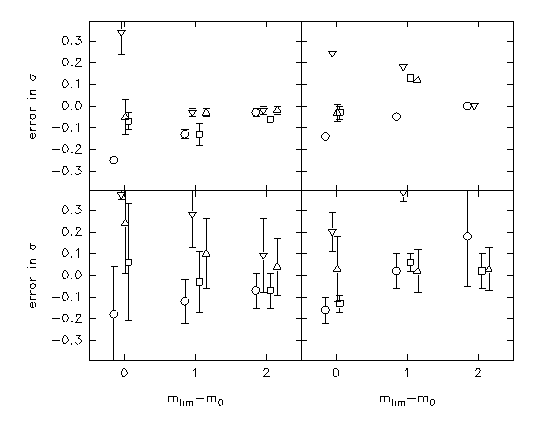
Figure 2 shows the errors in the adjustment of 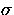 . Top panels
correspond to a very low contamination case, m0=23.35 and
Ngc=10000. The results displayed in the bottom panels correspond
to a high contamination case, with m0=24.75 and Ngc=400. This is
equivalent to observed counts of Nobsgc=365 and Nobsbkg=300 for
mlim =m0+2, and to Nobsgc=300 and Nobsbkg=100 objects for mlim =m0+1.
Left and right panels concern respectively to gaussian and t5
distributions. Different symbols stand for distinct starting
guesses.
. Top panels
correspond to a very low contamination case, m0=23.35 and
Ngc=10000. The results displayed in the bottom panels correspond
to a high contamination case, with m0=24.75 and Ngc=400. This is
equivalent to observed counts of Nobsgc=365 and Nobsbkg=300 for
mlim =m0+2, and to Nobsgc=300 and Nobsbkg=100 objects for mlim =m0+1.
Left and right panels concern respectively to gaussian and t5
distributions. Different symbols stand for distinct starting
guesses.
3.- And where is the turn-over?
It is needed to surpass clearly the turn-over to obtain
reliable estimates of m0. If m0=mlim , the resulting fitted
parameters are affected by significant systematic errors. If
m0-mlim =-1, then the errors in m0 estimates tend just to -1, that
is, it is not possible to distinguish between the true turn-over
and the drop of completeness.
Figure 3 displays the errors in the determination of m0. Top
and bottom panels show respectively the above mentioned cases of
low and high contamination. Circles and inverted triangles
represent gaussian fittings performed on gaussian and t5
distributions respectively. Squares and triangles indicate t5
fittings to gaussian and t5 distributions.
REFERENCES
Hanes & Whittaker, 1987, AJ, 94, 906
Harris, Allwright, Pritchet & van den Bergh, 1991, ApJS, 76, 115
Secker & Harris, 1993, AJ, 105, 1358



Next: About this document ...
Pablo Ostrov
1/11/1999